合成の人になじみ深い数平均分子量と、物性の人になじみ深い重量平均分子量。それぞれ、実際にどうやって求まるのか？などを簡単に数値を入れながら考えてみます。（それぞれの平均分子量の正確な表現は手元にある講談社ｻｲｴﾝﾃｨﾌｨｯｸのエッセンシャル高分子（第４刷）のものが最後に書いてあります。）
まず、数平均分子量（Mn）と重量平均分子量（Mw）の定義は簡単に書くならば、Mnが単純な分子1本あたりの分子量の平均、Mwが高分子量のものを重視するようにした平均分子量です。Mnは単なる平均なので、あまり深く考えなくても良いのですが、Mwはあまり普段こういう平均を取らないので感じをつかめない人も多いでしょう。
合成系の人がMnを気にするのは、多くの場合「ある量（X)のモノマーとある量（Y)の開始剤を加えた重合に、平均すると一本あたりのポリマー鎖はどれくらいのモノマー単位からできるのだろう？」という反応に対する興味があるからと言えます。たとえば、X=１００、Y=１なら平均的には１００量体ができるはずですが、実際にはどちらかが完全には消費されなかったり、同時性が低かったりして、このとおりになることは限られたケース（リビング重合など）のみです。
物性は一般にMnよりもMwに依存します。例えばガラス転移点などは普通Mwと温度の関係を取ったりします。では、なぜ高分子量体を重視したMwを使う必要があるのでしょうか？
そこで、それぞれの求め方と意味を実際に単純化した数値を使って考えて見ましょう。
まず、以下の図のような分子量の分布をもつポリマーの集まりについて考えます。
分子量 １００００ が3本
分子量 ５０００ が10本
分子量 １０００ が10本
このポリマーの集まりのGPCをとると下の図のようになるはずです。
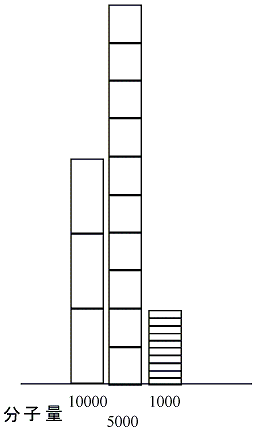それぞれ一つの枠が1本のポリマーこのポリマーの集まりのMnは以下の式で表すことができます。
Mn＝[10000 x 3(本） + 5000 x 10 (本) + 1000 x 10 (本)] / [3 + 10 + 10 (本)]
＝90000 / 23
＝3913
また、このときのMwは以下の式で表されます。
Mw＝[10000 x 10000 x 3(本） + 5000 x 5000 x 10 (本) + 1000 x 1000 x 10 (本)] / [10000 x 3(本） + 5000 x 10 (本) + 1000 x 10 (本)]
＝[300000000 + 250000000 + 10000000] / 90000
＝560000000 / 90000
＝6222
ぱっと見で一番多い５０００よりもちょっと小さいMnとちょっと大きいMwという結果になりました。ちなみにこの場合のMw/Mnは1.59です。全体の感じから見て、一番面積を占めているのが5000で、次に面積を占めているのが10000なのに、平均分子量が5000以下になるのはちょっと違和感を感じる人もいるかもしれません。
では、もう少し極端な場合を考えて見ましょう。
分子量 １００００ が3本
分子量 ５０００ が10本
分子量 １０００ が10本
分子量 １００ が10本
これは先ほどの例に分子量１００がさらに１０本ある場合です。このときの予想されるGPCプロファイルは以下のとおりです。
分子量１００は真っ黒になってしまいましたが１０本います。ぱっと見の印象は最初のもののGPCとあまり変わらないのではないでしょうか？このポリマーの集まりのMnは以下の式で表すことができます。
Mn＝[10000 x 3(本） + 5000 x 10 (本) + 1000 x 10 (本) + 100 x 10 (本)] / [3 + 10 + 10 + 10 (本)]
＝91000 / 43
＝2116
また、このときのMwは以下の式で表されます。
Mw＝[10000 x 10000 x 3(本） + 5000 x 5000 x 10 (本) + 1000 x 1000 x 10 (本) + 100 x 100 x 10 (本)] / [10000 x 3(本） + 5000 x 10 (本) + 1000 x 10 (本) +100 x 10 (本)]
＝[300000000 + 250000000 + 10000000 + 100000] / 91000
＝560100000 / 91000
＝6154
最初の場合と比べてポリマーの本数が増えている分Mnが約2/3と大幅に減りましたが、Mwはほとんど変わりません。このときのMw/Mnは2.91です。
このMwがあまり変わらないのは、分子量が１００００や５０００のポリマーが全体に占める割り合いはほとんど変わらないためです。つまりMwは「全体に対して占める割合を考慮した平均分子量」と考えると良いかもしれません。実際、全体としての性質は、体積の多いものが重視されるので、物性はおもにMwに依存するわけです。
